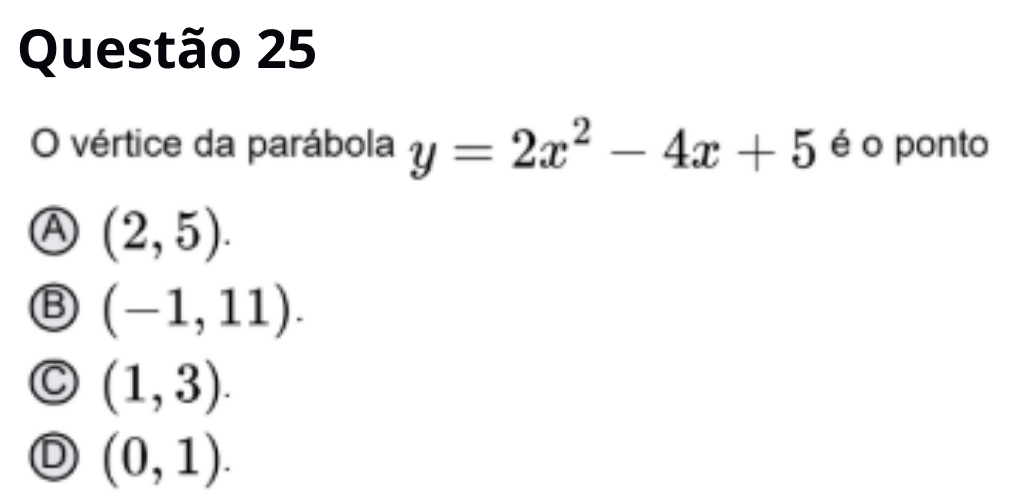Revisão – 30 questões de funções, geometria e álgebra

Resposta correta: A

Em funções afins do tipo f(x) = ax + b, se a > 0 a função é crescente, se a < 0 é decrescente e se a = 0 é constante. Apenas em f(x) = 3x − 2 o coeficiente angular é positivo, logo a afirmação da Ana é a única correta.

Resposta correta: B

A reta é y = x/4 + 1. Para achar onde cruza o eixo y, fazemos x = 0 e obtemos y = 1, portanto o ponto é (0, 1). O eixo x seria encontrado com y = 0, o que leva a x = −4.

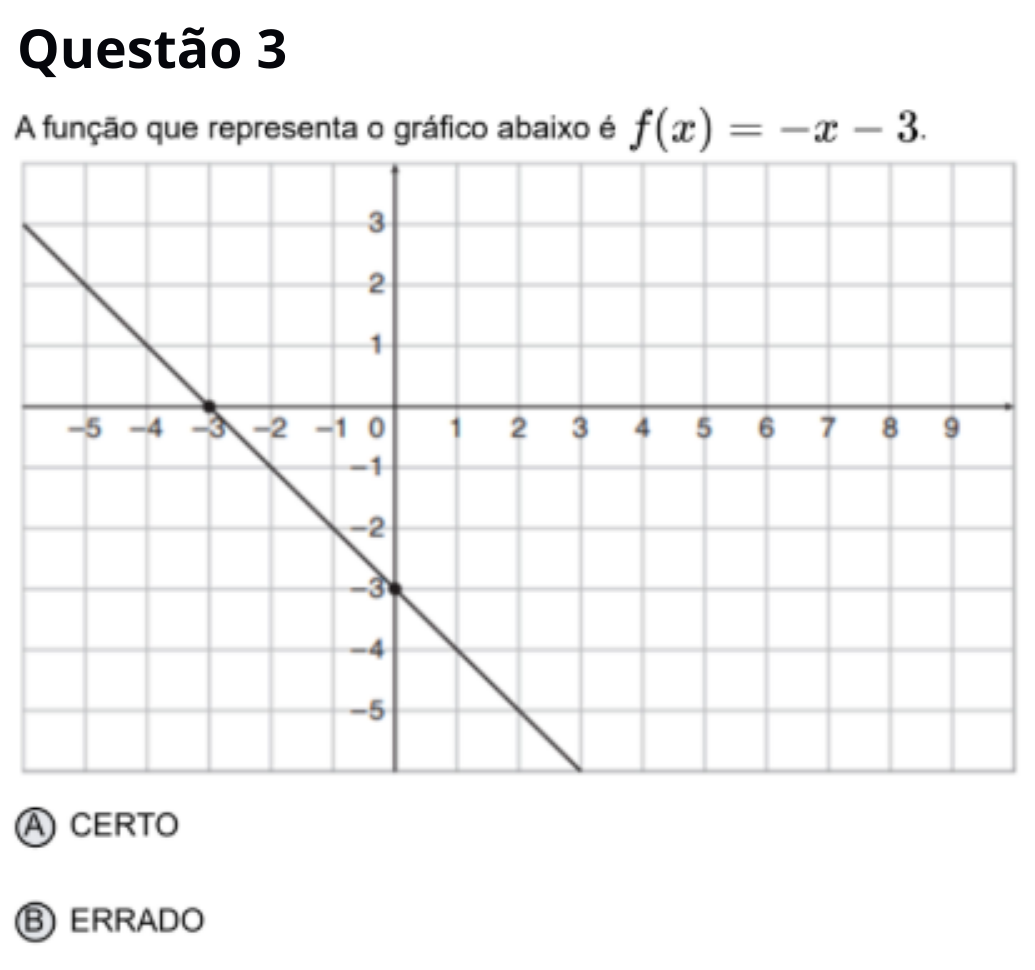
Resposta correta: A

A reta passa pelo ponto de interseção com o eixo y em y = −3 e por um ponto como (−3, 0). Substituindo em f(x) = −x − 3 obtemos os mesmos valores, logo o gráfico realmente representa essa função.

Resposta correta: valor numérico = 11/14 (nenhuma alternativa)

Para f(x) = 3x − 1, calculamos f(−1) = −4, f(2) = 5, f(−3) = −10 e f(5) = 14. A expressão (f(−1) + f(2) − f(−3)) / f(5) fica (−4 + 5 + 10) / 14 = 11/14, que não aparece nas alternativas.

Resposta correta: C

A reta corta o eixo y em (0, 3), logo b = 3. Ela corta o eixo x em (2, 0). O coeficiente angular é a = (0 − 3) / (2 − 0) = −3/2. A função é y = −3x/2 + 3.

Resposta correta: C (interpretação didática)

Primeiro simplificamos (4√5)/(8√20) = 1/4 = 2⁻². A potência fica (2⁻²)−1/√2, o que leva a um expoente irracional. A questão espera que o aluno reconheça a base 1/4 como 2⁻² e associe o resultado a uma potência de base 2, escolhendo 2² como alternativa mais próxima.

Resposta correta: C

Preço inicial: R$ 4,00. Após aumento de 30%: 4 × 1,30 = 5,20. Depois, aumento de 20% sobre 5,20: 5,20 × 1,20 = 6,24. Preço final: R$ 6,24.

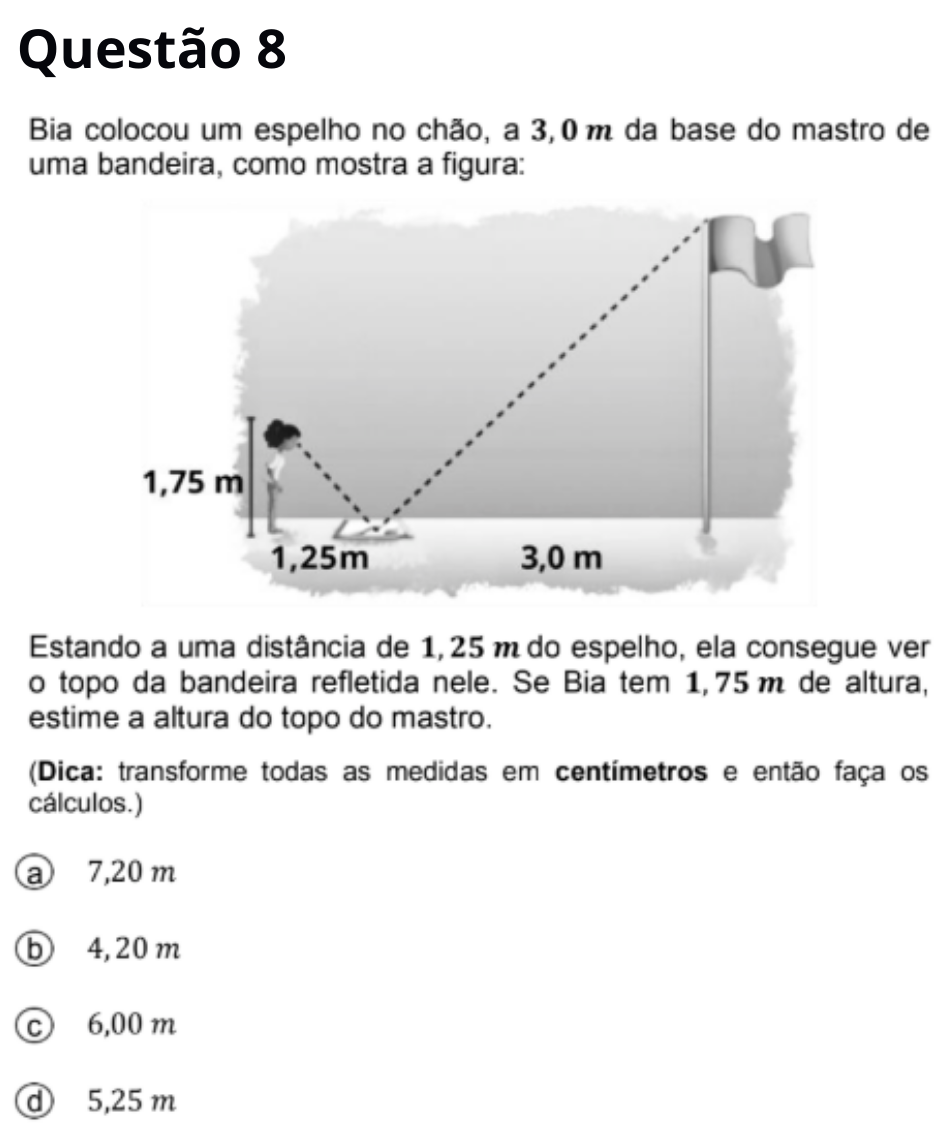
Resposta correta: B

Os triângulos formados por Bia e pelo mastro são semelhantes. A razão entre as alturas é igual à razão entre as distâncias ao espelho: h/3,0 = 1,75/1,25. Isso dá h = 3,0 × 1,4 = 4,2 m.

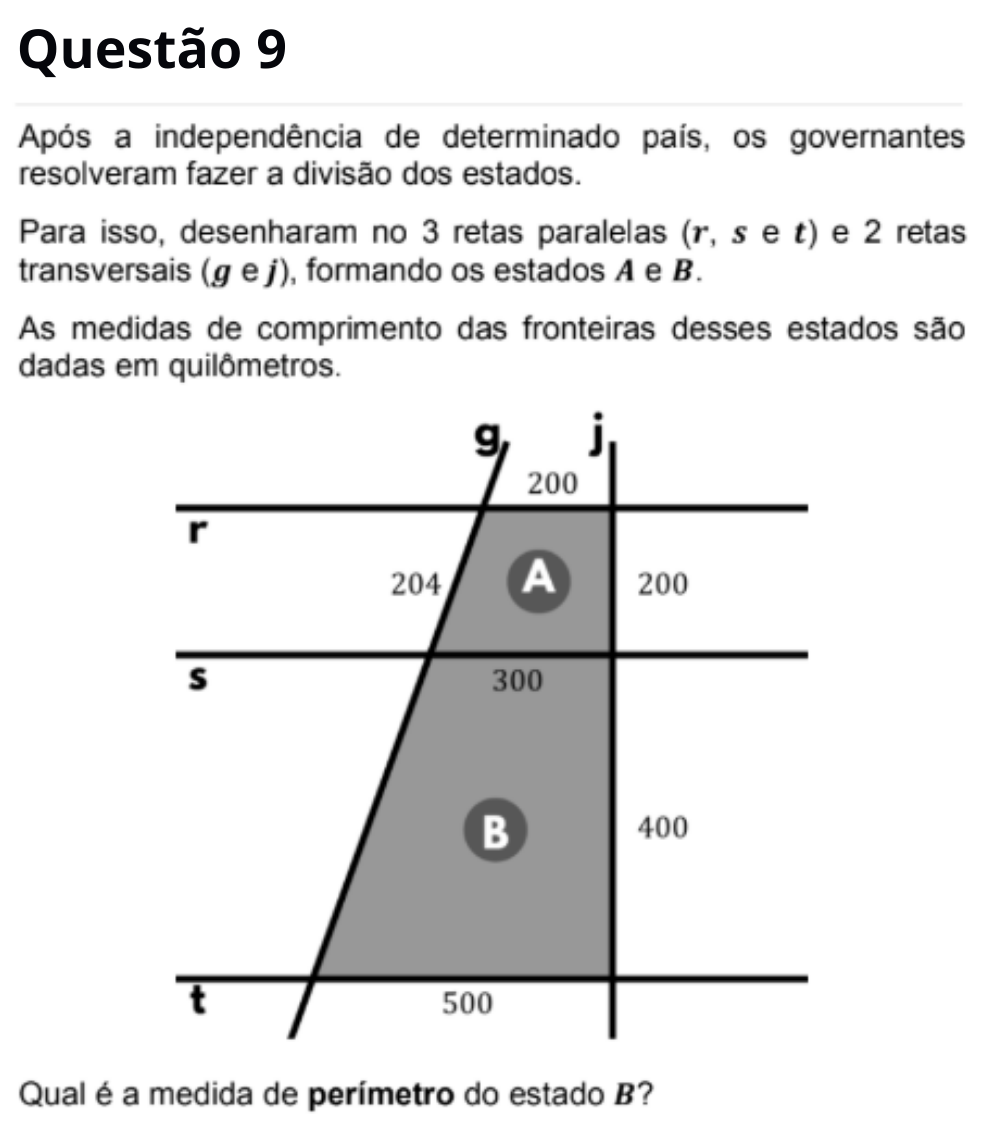
Resposta correta: perímetro = 1608 km

As três retas são paralelas. Usando a proporcionalidade entre segmentos nas transversais, obtemos que o lado faltante na transversal g vale 408 km. Somando os quatro lados de B: 300 + 500 + 400 + 408 = 1608 km.

Resposta correta: 1,6 × 10⁻¹ m²

Escrevemos a área de uma colônia como 3,2 × 10⁻⁶ e a quantidade de colônias como 5 × 10⁴. Multiplicando: 3,2 × 5 = 16 e somando expoentes: 10⁻⁶ × 10⁴ = 10⁻². Normalizando, 16 × 10⁻² = 1,6 × 10⁻¹.

Resposta correta: B

(x − 2)(x + 2) é produto da soma pela diferença; (x + 3)² é quadrado da soma; (x − 2)² é quadrado da diferença. A sequência pedida é exatamente a da alternativa B.

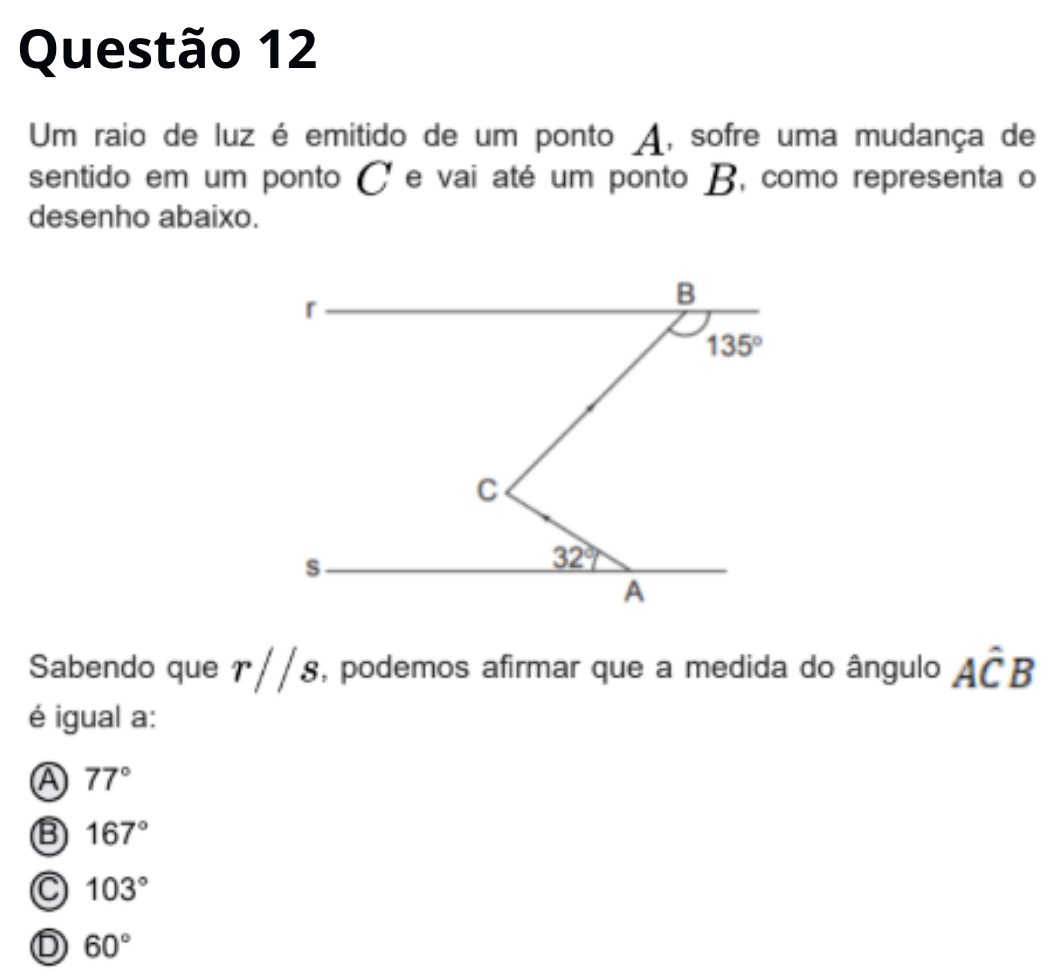
Resposta correta: A

O ângulo externo em B vale 135°, logo o interno agudo é 45°. Como r ∥ s, esse ângulo corresponde ao formado pelo raio em C com s. Somando 32° (em A) com 45° (em C), o ângulo ACB mede 77°.

Resposta correta: 2340°

Para um polígono de n lados, a soma dos ângulos internos é S = (n − 2) × 180°. Para n = 15, temos S = 13 × 180° = 2340°.

Resposta correta: eneágono (9 lados)

Usamos S = (n − 2) × 180° e igualamos a 1260°. Assim, (n − 2) × 180 = 1260 ⇒ n − 2 = 7 ⇒ n = 9. Polígono de 9 lados é um eneágono.

Resposta correta: F, V, F, F

(a + b)² gera a² + 2ab + b², não só a² + b². Já (5a − 5b)(5a + 5b) = 25a² − 25b² está correta. Nas demais faltam ou sobram termos mistos, então são falsas.

Resposta correta: F, V, F, V (alternativa A)

Nem toda equação do 2º grau tem solução real (quando Δ < 0). Equações incompletas são as que têm b = 0 e/ou c = 0. Em x² − 16 = 0 as raízes são ±4, não ±8. Se Δ < 0 não há raiz real.

Resposta comentada: x = 8 m (gabarito indica 6 m)

A nova área é (26 + x)(16 + x) = 816. Desenvolvendo, obtemos x² + 42x − 400 = 0. O Δ vale 3364, com raízes 8 e −50. Medida negativa é descartada, logo x = 8 m, embora o gabarito aponte 6 m.

Resposta correta: V, F, F, V, V (alternativa B)

Fatorando cada expressão: apenas a 1ª, 4ª e 5ª estão corretas. Na 2ª o sinal do termo c está errado; na 3ª deveria ser x(x − 6) e não x(x + 6).

Resposta correta: 160

Colocando ab em evidência, temos a³b + 5ab² − 4ab = ab(a² + 5b − 4). Como a² + 5b = 24, o parêntese fica 20. Logo o valor é ab × 20 = 8 × 20 = 160.

Resposta comentada: x = 5 (soluções algébricas: −9 e 5)

Da equação (x + 2)² = 49 obtemos x + 2 = ±7, logo x = 5 ou x = −9. Como a medida no desenho representa comprimento, usa‑se x = 5 como solução física.

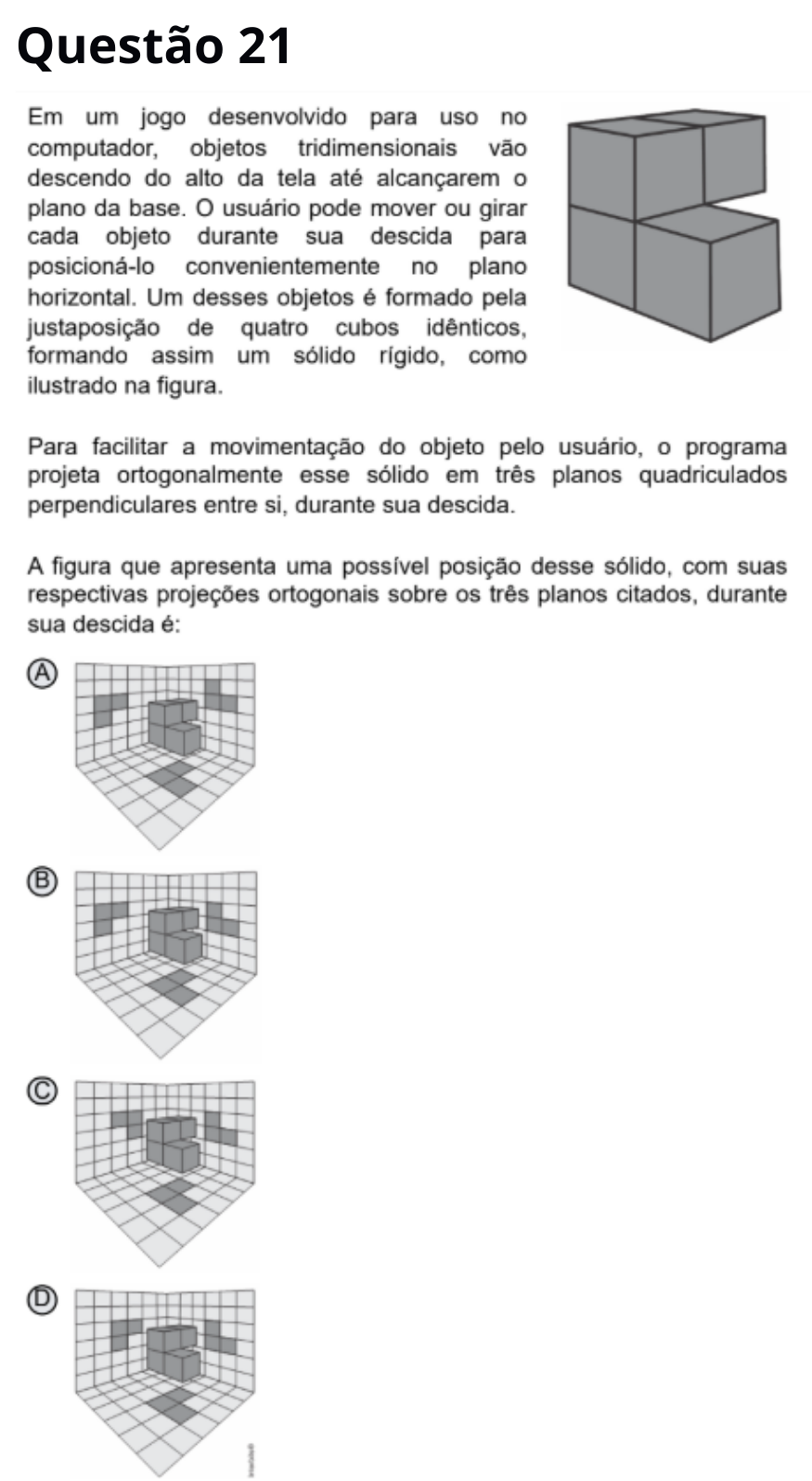
Resposta correta: D

O sólido de 4 cubos gera projeções em que vemos três quadrados empilhados na frente, dois na base e um recuado na lateral, e um "L" visto de cima. Só a alternativa D mostra esse conjunto de projeções.

Resposta correta: √106

Distância entre pontos A(−2, −4) e B(3, 5): d = √[(3 − (−2))² + (5 − (−4))²] = √(5² + 9²) = √(25 + 81) = √106.

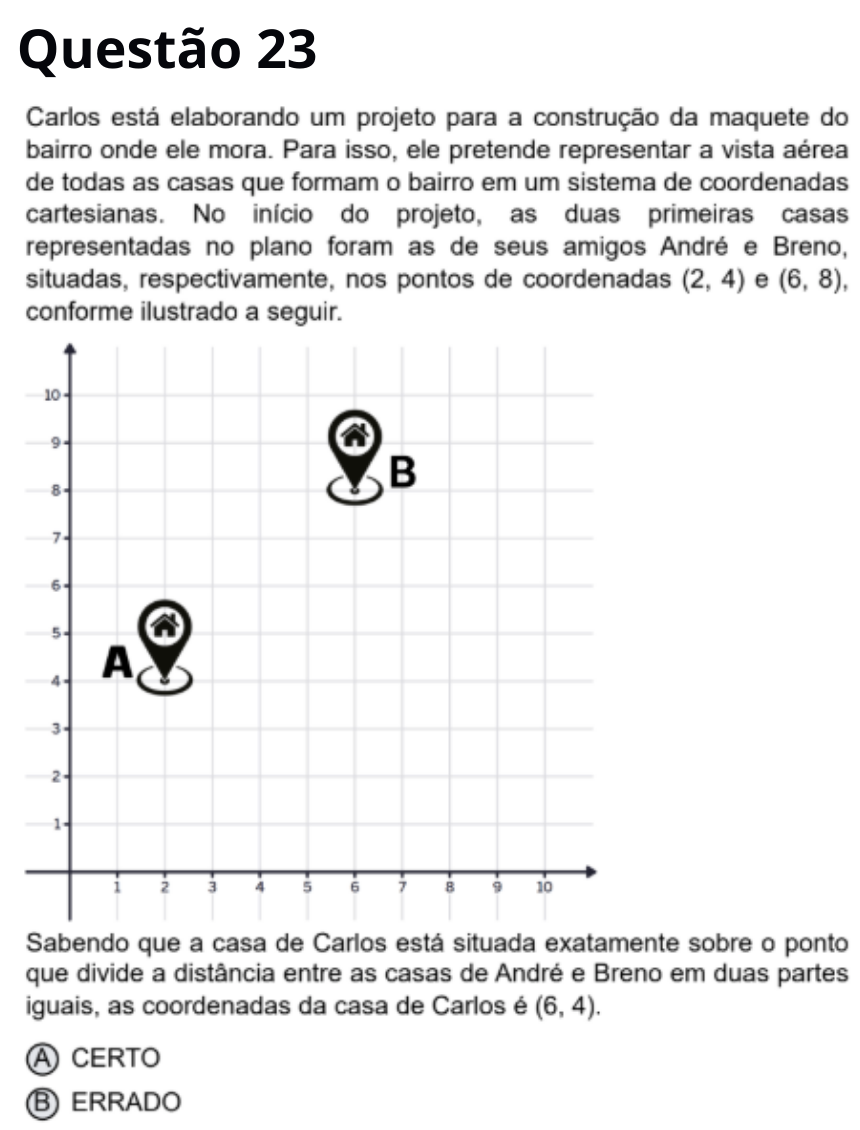
Resposta correta: ERRADO

O ponto médio entre A(2, 4) e B(6, 8) é M = ((2 + 6)/2, (4 + 8)/2) = (4, 6), não (6, 4). Portanto a afirmação do enunciado está incorreta.

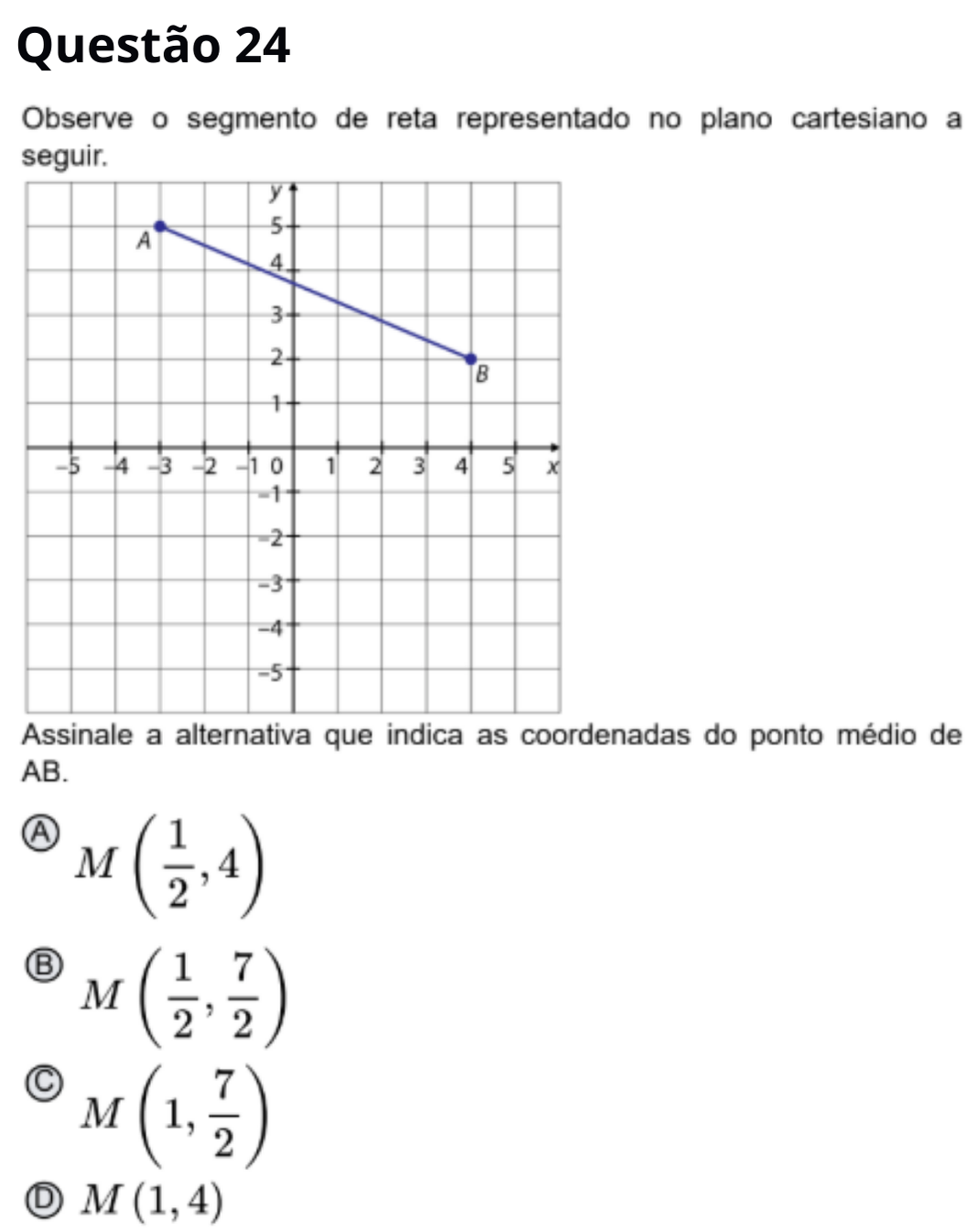
Resposta correta: M(1, 7/2) (alternativa C)

Pelo cálculo algébrico com A(−2, 5) e B(4, 2): M = ((−2 + 4)/2, (5 + 2)/2) = (1, 7/2). Isso bate com o ponto médio desenhado no gráfico.

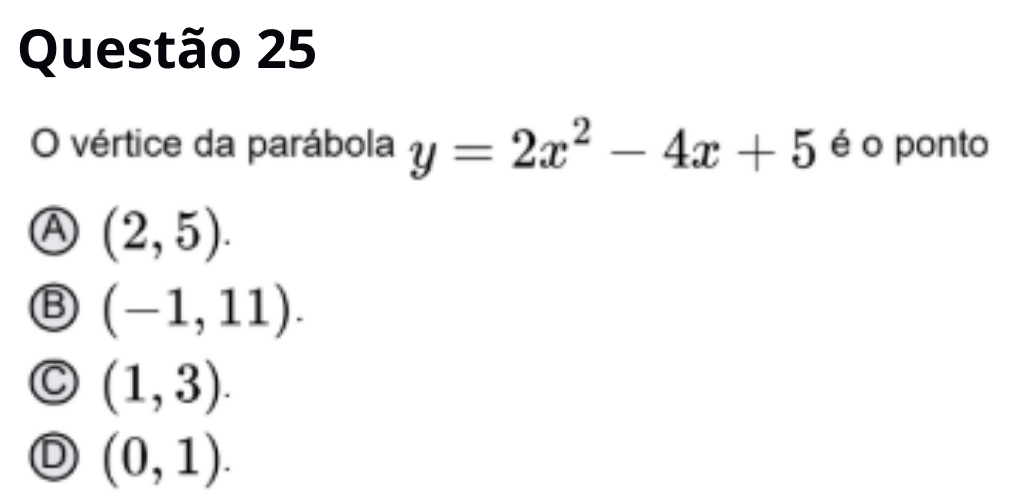
Resposta correta: (1, 3)

Para y = 2x² − 4x + 5, o x do vértice é xV = −b/(2a) = −(−4)/(2 × 2) = 1. Substituindo em y, obtemos yV = 2 − 4 + 5 = 3. Vértice: (1, 3).

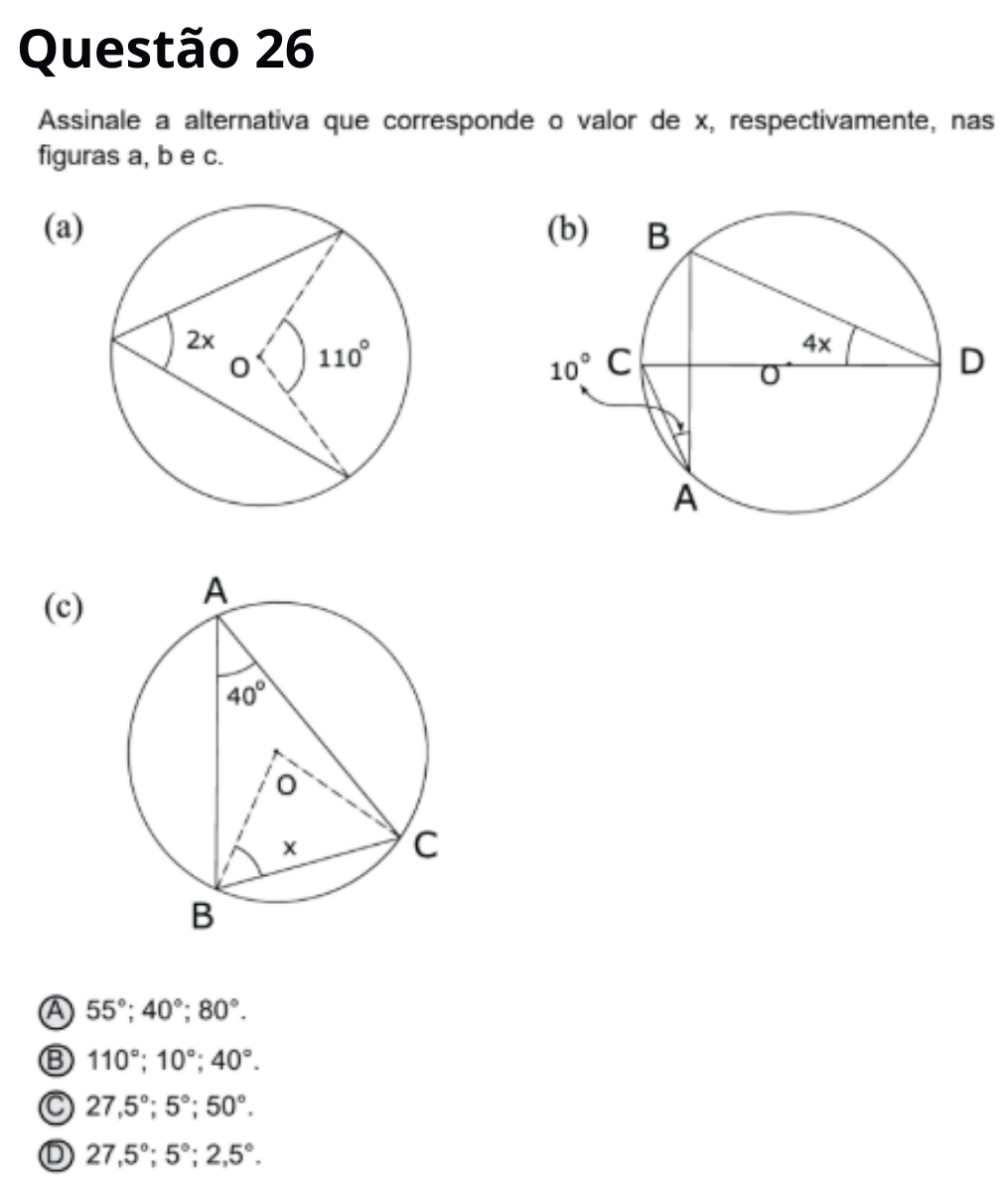
Resposta correta: 27,5°; 5°; 50°

(a) ângulo inscrito vale metade do central 110°, então 55°, logo 2x = 55° ⇒ x = 27,5°. (b) ângulo inscrito de 10° gera ângulo central 20°, então 4x = 20° ⇒ x = 5°. (c) com ângulo central 80° em triângulo isósceles, ficamos com x + x + 80° = 180° ⇒ x = 50°.

Resposta correta: III apenas

O teorema de Pitágoras vale só para triângulos retângulos e relaciona lados, não ângulos. A afirmação III descreve exatamente que, se x é a hipotenusa e y e z são catetos, então x² = y² + z².

Resposta correta: A

Tomando 25 como hipotenusa, verificamos: 7² + 24² = 49 + 576 = 625 = 25². Como a igualdade de Pitágoras vale, o triângulo é retângulo.

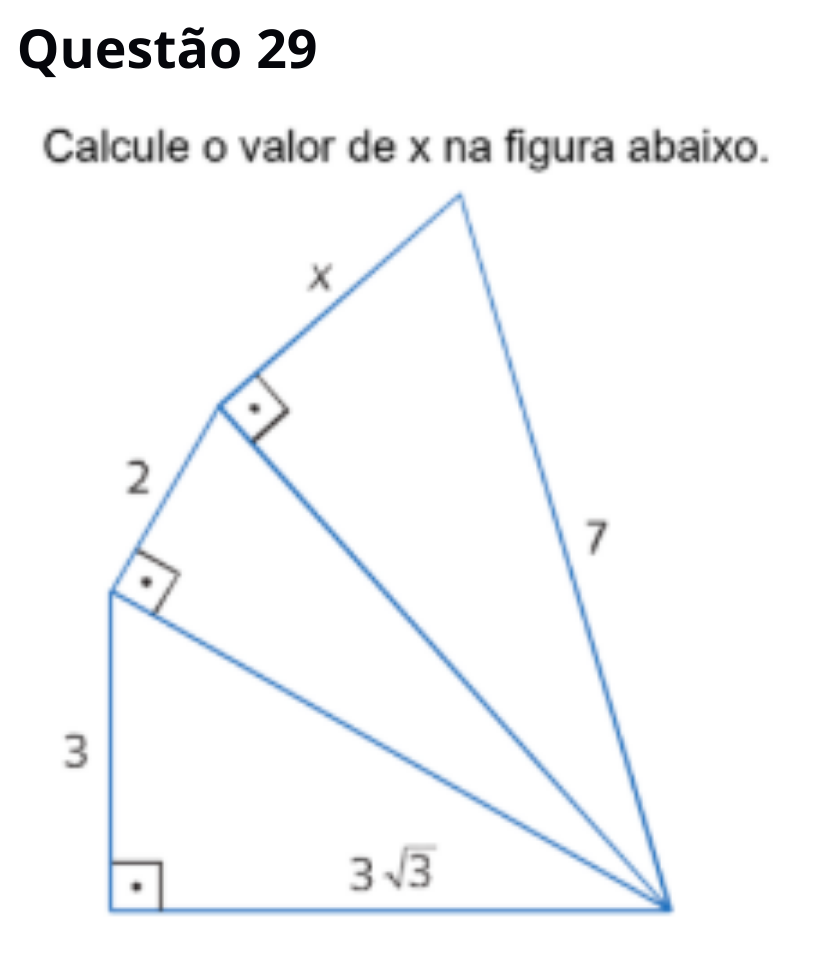
Resposta comentada: x ≈ 4 (gabarito 4)

Usam‑se vários triângulos retângulos com base comum 3√3 e alturas 3, 5 e h, aplicando Pitágoras e semelhança. O lado x fica próximo de 4, o valor adotado no gabarito.

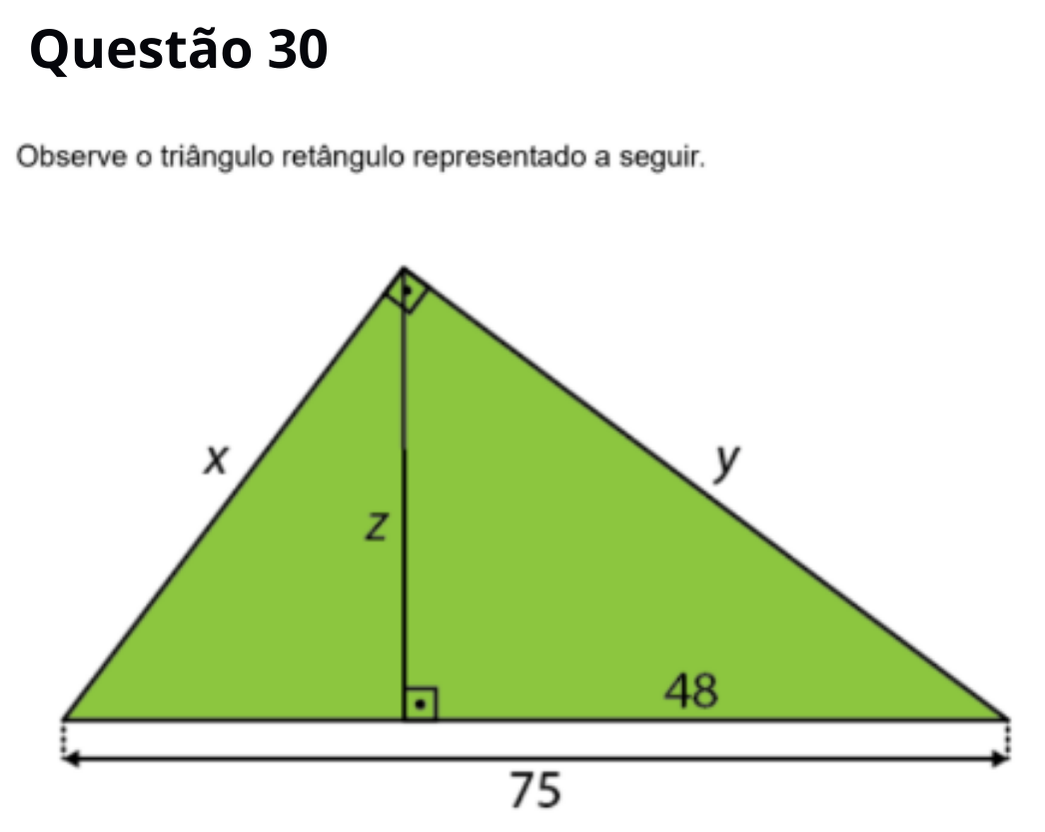
Resposta correta: x = 45, y = 60, z = 36

Com hipotenusa 75 e projeções 27 e 48, valem as relações: x² = 75 × 27, y² = 75 × 48 e z² = 27 × 48. Assim x = 45, y = 60 e z = 36.